Recently, a post was published on Search Engine Journal, authored by Aysun Akarsu, on the notion of Harmonic Centrality – one of several measures of closeness, or centrality, to important nodes in graph theory.
The piece discussed the viability of this measure as a potential alternative ranking algorithm to PageRank – in that graph theory nodes and edges are like webpages and links.
Intriguing & Insightful
I thought the piece was excellent – very insightful, and thought-provoking.
The piece intrigued me, so I went off to Google Scholar to run some searches on “harmonic centrality” and find out more.
Other Papers Touching on Harmonic Centrality
I came across a few papers which seemed like they might also be relevant to it (one of which had been cited by Akarsu):
- Axioms for Centrality
- Graph structure in the web revisited – a trick of the heavy tail
- The Graph Structure in the Web – Analyzed on Different Aggregation Levels
Some of these papers seem quite old and they don’t have a lot of citations (certainly not in the range of thousands), which made me think that this hadn’t been implemented at scale (i.e., adopted by major search engines as yet), since more would be referencing it, particularly as they are likening it to PageRank.
Axioms for Centrality
One of the results returned in Google Scholar had been cited in the piece by Akarsu – a 2013 research paper by Paolo Boldi and Sebastiano Vigna entitled ‘Axioms for centrality’.
Their work was undertaken as part of an analytical study of link graphs comparing various algorithmic methods and their output effectiveness when seeking to understand the most important nodes in a network, utilizing “centrality.”
A General-Purpose Centrality Index?
Whilst this study, in particular, was carried out on a social network, to identify the most important points in the network, according to Boldi and Vigna, they claimed in their findings that Harmonic Centrality could potentially be extended as a general-purpose centrality index for arbitrary directed graphs, and as Akarsu quoted:
“Our results suggest that centrality measures based on distances, which in the last years have been neglected in information retrieval in favour of spectral centrality measures, do provide high-quality signals; moreover, Harmonic Centrality pops up as an excellent general-purpose centrality index for arbitrary directed graphs.” (Boldi & Vigna, 2013).
Boldi and Vigna also find:
“Surprisingly, only a new simple measure based on distances, harmonic centrality, turns out to satisfy all axioms; essentially, harmonic centrality is a correction to Bavelas’s classic closeness centrality designed to take unreachable nodes into account in a natural way.”
Professor Ricardo Baeza-Yates
Intrigued further, I reached out to Professor Ricardo Baeza-Yates, to ask what his thoughts were on the notion of harmonic centrality as an alternative to PageRank, as I thought it would be useful to get additional informed opinions.
I asked Baeza-Yates because he is the author of ‘Modern Information Retrieval’, a core text-book on information retrieval (cited over 17,000 times by both academics and industry practitioners of the search-engineer world), and also ex-VP of Research at Yahoo Labs.
Computational Expense
Baeza-Yates’s initial thoughts were that, (with regards to the computational expense involved):
“My first issue would be that computing centrality measures in large graphs is VERY expensive as it is not a local linking measure.”
Therefore, his thoughts were that harmonic centrality would be slower to compute than PageRank.
I shared Akarsu’s article with him, to which he replied, after reading:
“Interesting article, according to this it is as easy as computing PageRank. I know Paolo (Boldi) and Sebastiano (Vigna). I will ask them first.”
Baeza-Yates was referring to ‘Axioms of Centrality’ research cited by Akarsu in the article. Since he knew the authors he was going to discuss the papers, theories, and experiments with Boldi and come back to me.
I also asked Baeza-Yates about the following in relation to the size of the dataset, because it seemed to make sense there could be value for smaller projects not as huge as the web itself – for example, within enterprise (or smaller) sites:
“How about within an individual site to e.g., compute something similar to PageRank within the domain itself? I am thinking from an internal equity perspective locally, say on a large site (e.g. 1 million+ pages), rather than the scale of the web. Presumably it could have some value for enterprise sites to get ideas of strengths in various site sections with this measure?”
Websites Are Trees
Baeza-Yates’s response:
“Websites are trees which are very different from typical web structures at the domain level. For websites it would be better to define a completely new measure which is not related to centrality but more about distance to the root, semantic cohesion, etc. For example, does anyone knows what exactly characterizes a good website? What link structure should it have?”
My response:
“I see a lot of varying opinion on optimal sites structures – flat or with hierarchical categories and silos. I prefer hierarchical flattened via jump pages to shorten click paths and sibling links as well as the child relationships. There are others who are adamant with topical silos.”
The Bow Tie of the Web
On the topic of the link graph of the web itself (and the structure of the web overall), I raised the question of whether Baeza-Yates considered the shape of the web still to be like a bowtie from the “The Bowtie of The Web”.
The “bowtie of the web” comes from a 2000 paper by Broder et al, Graph Structure in the Web (cited by thousands, and if you have not read this it is a recommended reading).
The central point on the bowtie is “the strongly connected component” (a central point with many links in and out).
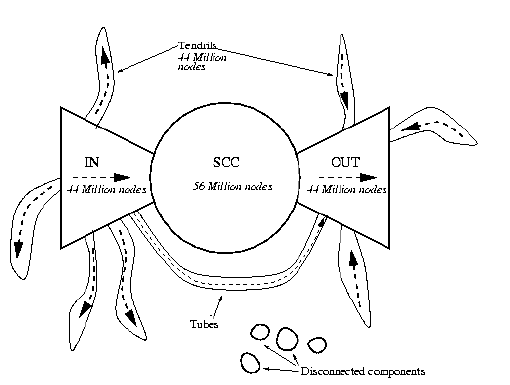
Baeza-Yates made the point:
“It should still be a bow tie. There was a paper that shows that the IBM website which was very large also had this structure but also had other characteristics (and an old paper now, more than 10 years old). Today most websites are fully dynamic or a great percentage of it is dynamic and that also implies a different link structure., so the structure is not that important. What is important is findability!”
He also clarified my queries about Harmonic Centrality from a distance perspective:
My question:
“If I’m not mistaken harmonic centrality appears to simply be a measure of distance from a strongly connected component?”
His answer:
“It is a measure of ‘inverse distance’ (that is why it is called harmonious, as this comes from a harmonic average) from all other nodes connected to a node, so all of them have to be in a connected component. If the diameter is too large, the complete paths will be too long. On the other hand, as you are adding terms of weight proportional to 1/distance, the contributions are smaller each time (but not negligible as the sum of 1/i does not converge, as that grows like log(n)), where n is the number of terms in the sum. This is one main difference with PageRank, where each time you multiply by q and q^i decreases much faster than 1/i.”
An Experiment to Compare: Pagerank vs. Harmonic
In the meantime Baeza-Yates had raised the question of the computational expense on larger datasets with Boldi, believing that Harmonic Centrality would be slower to compute, who then carried out an experiment as a result of that discussion and reports as follows:
“Paolo Boldi and Sebastiano Vigna ran a brief experiment on a small web dataset (84M pages). PageRank with alpha=0.85 required 1h of computation to get a L1-norm of the difference smaller than 10-6), whereas harmonic centrality required 14h (for a standard deviation of 4.6 percent). Let’s say one order of magnitude more (although it may be the case that, a larger standard deviation can be as good).”
They continued:
“The quality of results for harmonic centrality seems better. Try the website below and sort by PageRank and then by Harmonic to see the difference: http://wwwranking.webdatacommons.org/.”
Therefore, to conclude, further to the brief follow-up experiment by Boldi and Vigna following the discussion and comments by Baeza-Yates:
“Whilst Harmonic Centrality seems better for the results, the computing time is much longer.”
The experiment was done because of some comments that Baeza-Yates made to Boldi, whereby he believed that Harmonic Centrality would be slower to compute (which seems to be right).
Other Concerns
I asked Baeza-Yates if there were any other concerns and considerations with Harmonic Centrality versus PageRank, to which he replied:
“I think that is the main concern (computational expense). Another question would be which is easier to spam? I guess Harmonic centrality is more robust because it depends on longer paths (PageRank has an exponential decay while Harmonic Centrality has an harmonic decay).”
Link-Ranking Measures
Baeza-Yates also made the following interesting point:
“PageRank is overrated as a link-ranking measure and the same is true for any link-based measure as today there is so much link spam, before we had webmasters to add links. Today, anyone can add links. Click based signals are the best today.”
Either way, Akarsu was correct in that Harmonic Centrality is certainly something worth learning more about. It is certainly a topic I will be exploring further.
Test for yourself PageRank versus Harmonic Centrality via comparisons with the experiment created by Boldi and Vigna on Web Data Commons.
Thanks to Ricardo Baeza-Yates, Paolo Boldi, Sebastiano Vigna, and Aysun Akarsu.
More Resources:
- Can Harmonic Centrality Be the New PageRank?
- PageRank Patent Update – How it Impacts SEO
- 7 Useful Facts About PageRank
Image Credits
Screenshot taken by author, January 2019